Current and Past Research

Global epigenomic representations of genomic loci with a biologically-inspired foundation model

The folding patterns of chromatin produce a complex gene regulatory network that dictates gene transcription and is, in turn, influenced by the cellular processes driven by gene activity. Understanding the structure-function interplay of chromatin folding and gene transcription has the potential to lead to breakthrough technologies in a myriad of areas including drug discovery, cancer therapy, and cell reprogramming. Creating a concise set of features to represent and model a cell’s structure and function, however, has been challenging due to the high dimensionality, noise, and volume of biological data. Recently, researchers have seen success in adapting foundation models developed for natural language processing and computer vision to produce representations of biological entities such as cells and genes from a variety of assays spanning transcriptomics, proteomics, and epigenomics. While much of the work on biological foundation models have focused on areas where data are most abundant, such as RNA- and DNA-sequencing data, less attention has been devoted to models for cellular structure. Furthermore, nearly all foundation models for structure have relied on 1D epigenomic assays, which fail to capture interactions between genomic loci that are essential for understanding key aspects of cellular function, such as gene pathways and transcription clusters.

In this work, we present the first ever foundation model for global 2D chromatin structure. This model operates on Hi-C data, which captures pairwise chromatin interactions, across the entire genome to produce global representations of epigenomic structure for arbitrary genomic loci. The model is resolution-free, sparsity-leveraging, and biologically-informed. Once fully trained, this model can be integrated with existing foundation models for cellular function, offering new insights into the relationships between structure and function within the cell.

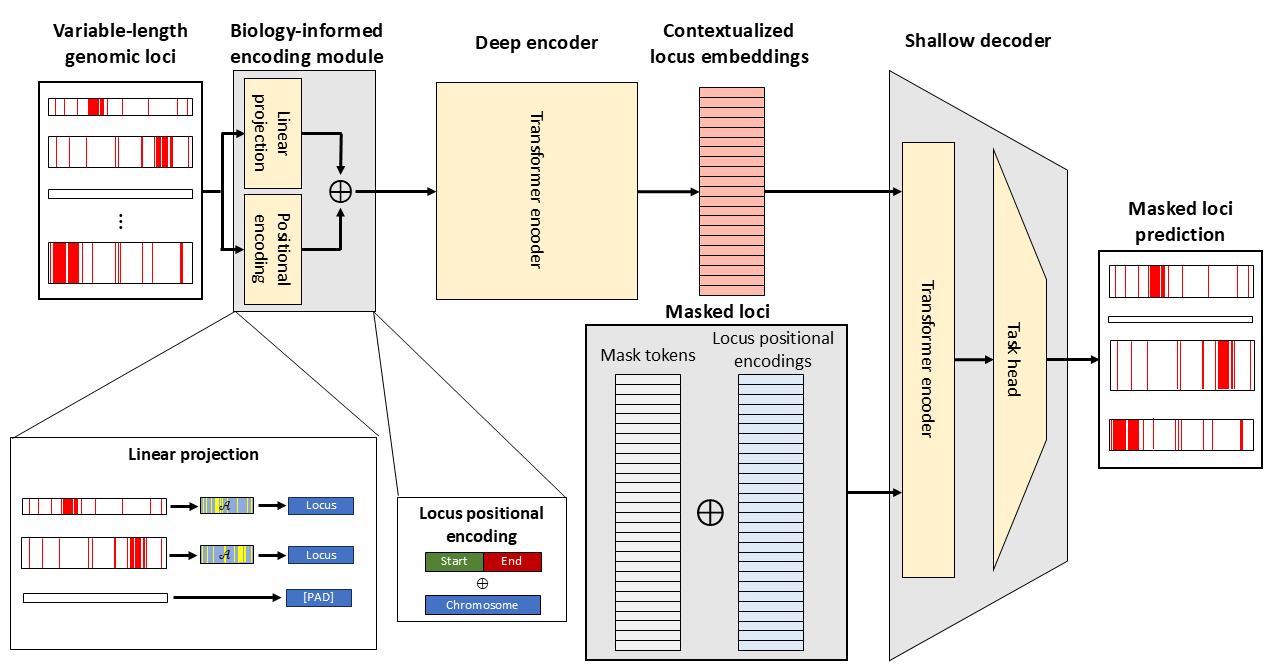A schematic of the proposed Hi-C foundation model architecture.

Estimation under uncertainty using probabilistic modeling [1, 2, 3]

To produce reliable estimates under uncertainty, the model, measurement, and parameter uncertainties must all be properly modeled. In the standard Bayesian system ID framework, measurement uncertainty is modeled as a noise term in the system output, parameter uncertainty is modeled as a posterior distribution over the parameters, but model uncertainty is neglected. To correct for this omission, my research accounts for model uncertainty by including a process noise term in the dynamics. Then, a recursive Bayesian filtering procedure can be used to evaluate the new likelihood created by this alteration in an efficient manner.

One benefit of this approach is that it is general enough to contain many other system ID objectives as special cases. By pinpointing the assumptions needed to derive other objectives from this general framework, one can identify the types of problems for which a given objective is best and worst suited. As examples, I have shown in [1] the assumptions needed to arrive at well-known algorithms such as the dynamic mode decomposition (DMD) and the sparse ID of nonlinear dynamics algorithm, better known as SINDy. Then, I numerically validated my theoretical observations by showing that these algorithms’ estimates incur greater error relative to the general approach when their corresponding assumptions are broken. An example result showing the posterior mean from the general framework significantly outperforming DMD on a simple linear system is given below. In a subsequent work [2], I also compared this Bayesian algorithm to a machine learning approach that had achieved state-of-the-art performance on a benchmark dataset containing 100,000 training data. After reducing the dataset to only 1,000 data points and adding noise, the Bayesian approach yielded 8.7 times lower mean squared error than the comparison method. This showed that even state-of-the-art machine learning methods can be greatly improved for small and noisy datasets by proper modeling of uncertainty. Overall, these results demonstrate the robustness of the probabilistic approach under uncertainty and illustrate how the framework can be used to offer a new perspective on the optimality of existing objective functions.

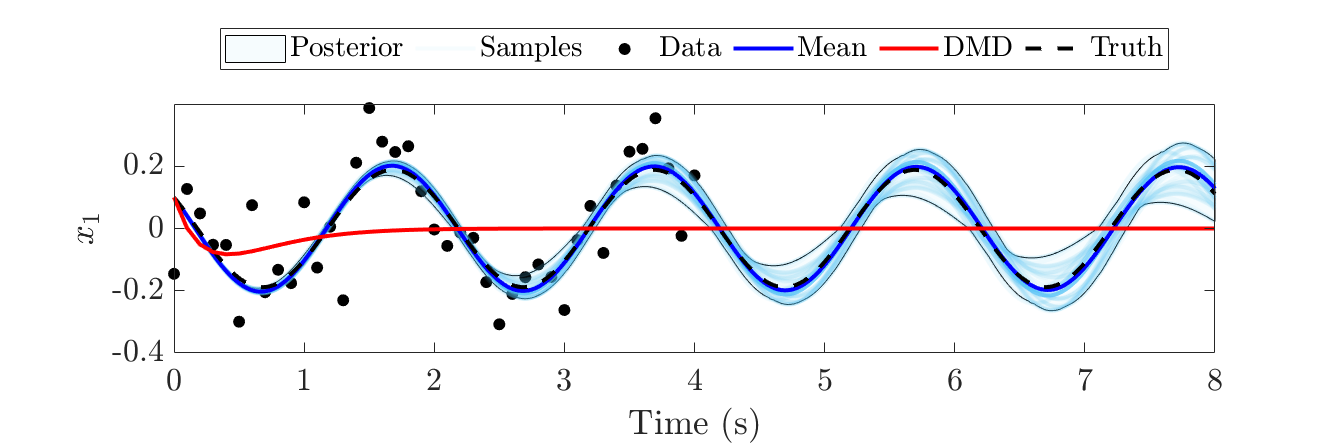The Bayesian approach greatly outperforms DMD on noisy data.

In addition to improvements in estimation accuracy, the use of a stochastic dynamics model for system ID delivers the following three unique benefits.

Novel measure of model complexity for regularization

Explicit regularization in parametric system ID often amounts to introducing an additive term penalizing some notion of the parameter vector size. For black-box models, e.g., neural networks, such terms are difficult to interpret due to the complex interactions between parameters and the non-uniqueness of parameter estimates. By using a stochastic dynamics model, I discovered that a regularization term arises naturally in the likelihood without the need for ad hoc approaches. This regularization term amounts to the determinant of the output covariance of the model. One benefit of this term is that it is more interpretable than parameter regularization because the output of a system typically carries physical meaning, unlike black-box parameters. The presence of this term results in a penalty on dynamics models that map nearby points farther apart, yielding a likelihood that favors dynamics that possess the simplest behavior needed to fit the data. The regularizing effect of this term was validated on numerical experiments in [2] that showed 3.87 times better root mean squared testing error compared to a likelihood without this term that had achieved lower training error. Therefore, the determinant of the output covariance can be interpreted as an effective measure of model complexity for regularization.

Precise tuning of likelihood smoothness

It is well-known in nonlinear system ID that there is a tradeoff between the smoothness of the objective function and assessing the accuracy of the long-term model behavior within the objective. Since objective function smoothness influences the success of optimization, it is common practice to tune the smoothness by introducing a truncation length hyperparameter. This hyperparameter specifies the maximum number of timesteps to consecutively evaluate the model before restarting evaluation at a different initial condition. The performance of this approach, however, strongly depends on careful selection of the truncation length. In [2], I showed that the process noise covariance has a similar smoothing effect as this hyperparameter, but with four main advantages. 1) The covariance is a continuous parameter that allows for more precise tuning than the discrete truncation length. 2) The covariance term can account for correlations between the components of the state for greater tuning flexibility. 3) The covariance enters directly into the likelihood and can therefore be tuned automatically during optimization or sampling. 4) Use of the covariance does not require the estimation of additional initial conditions.

Data-efficient quantification of model uncertainty

In many estimation approaches, it is impossible to know how good the estimated model is without testing it on a set of validation data. If the available dataset is small, however, it is preferable to utilize the full dataset for training rather than reserve a subset for validation. With a stochastic dynamics model, one can get a sense for the model quality without need for a validation dataset by interpreting the process noise covariance as a quantification of the model uncertainty. In [3], I showed through numerical experimentation that comparing the estimated process noise variances of two models was effective in accurately ranking the quality of those models with respect to prediction error.

Reducing data requirements through physics-informed modeling [3, 4]

When modeling physical systems, there is often more information known about the structure and characteristics of the system than that which is contained in the data. Typically, this additional information comes from physics knowledge such as conservation laws. Finding ways to encode this knowledge into the system ID framework is important for three main reasons. Models that follow the laws of physics are (1) more physically meaningful and interpretable, (2) generalize better outside the training data, and (3) require fewer data to train. Other works have validated these benefits numerically by comparing point estimates of physics-informed and non-physics-informed models. In [3,4], I provided a fresh perspective on physics-informed modeling through the lens of uncertainty. Specifically, I showed that using a structure-preserving integrator to evaluate the model during training not only yields more accurate estimates, as others have shown, but it also reduces the uncertainty of model predictions. The reduction in uncertainty was seen both quantitatively through an order of magnitude smaller process noise covariance and qualitatively in a more narrow spread of the outputs yielded by the parameter posterior. These experiments serve as numerical validation for the intuition that encoding physical knowledge into system ID improves model certainty and provide greater insight into the ways in which physics-informed modeling affects the estimation procedure.

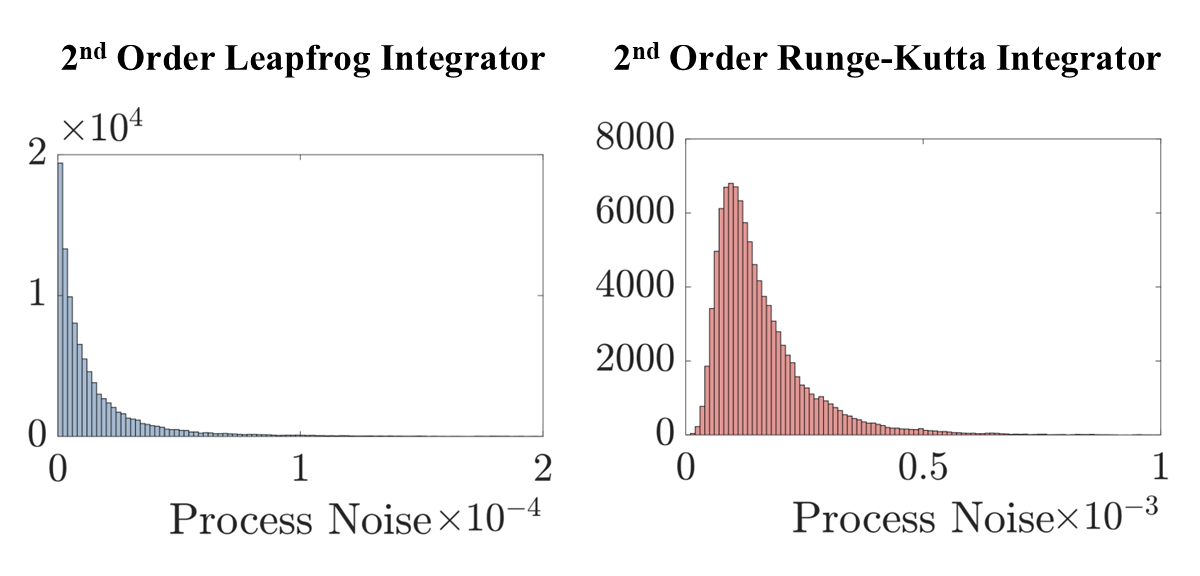The structure-preservation in the leapfrog integrator reduces model uncertainty by an order of magnitude.